Minkowski sums

Automating Label Placement in CAD Drawings Using Minkowski Sums and Convex Hulls for Obstacle Detection

Problem Description

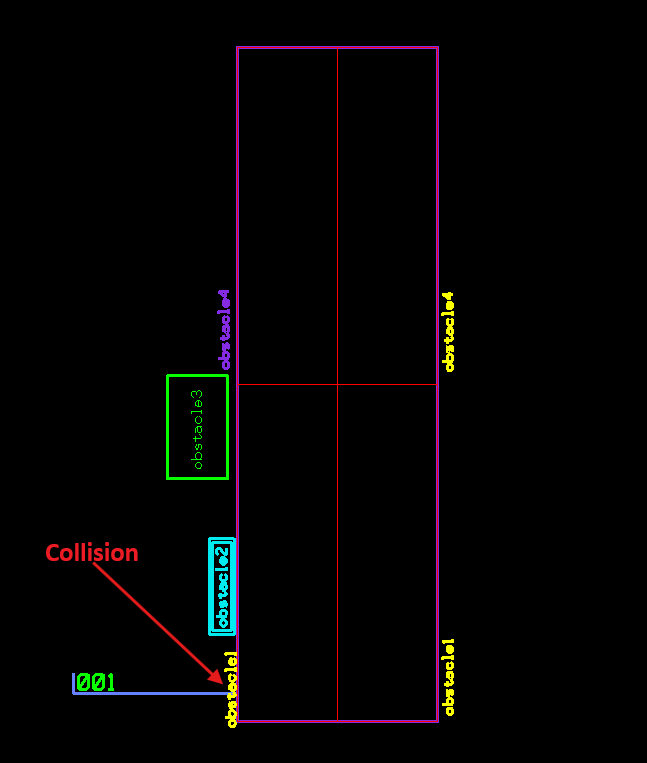
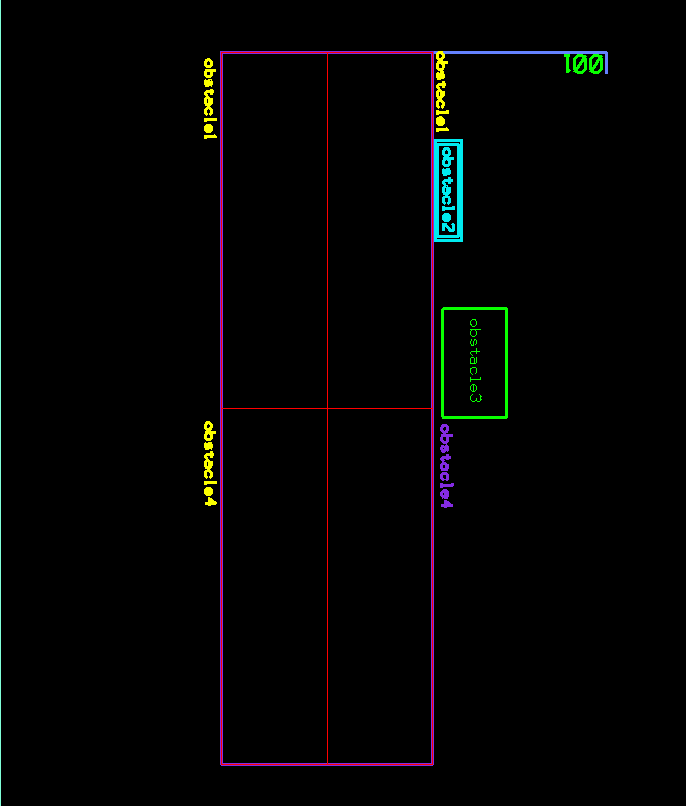
Placing labels and annotations in CAD drawings is typically a very tedious/manual and error prone process. Automating the placement of the label itself is relatively straightforward, but determining where to place it without interfering with existing graphical entities is an entirely new problem to solve.

Overview

To compute the collision-free placement of the new label for the example above we have developed a five step process outlined below using the Minkowski Sums and Convex Hulls algorithms from the Boost Geometry Library.

Quick definitions

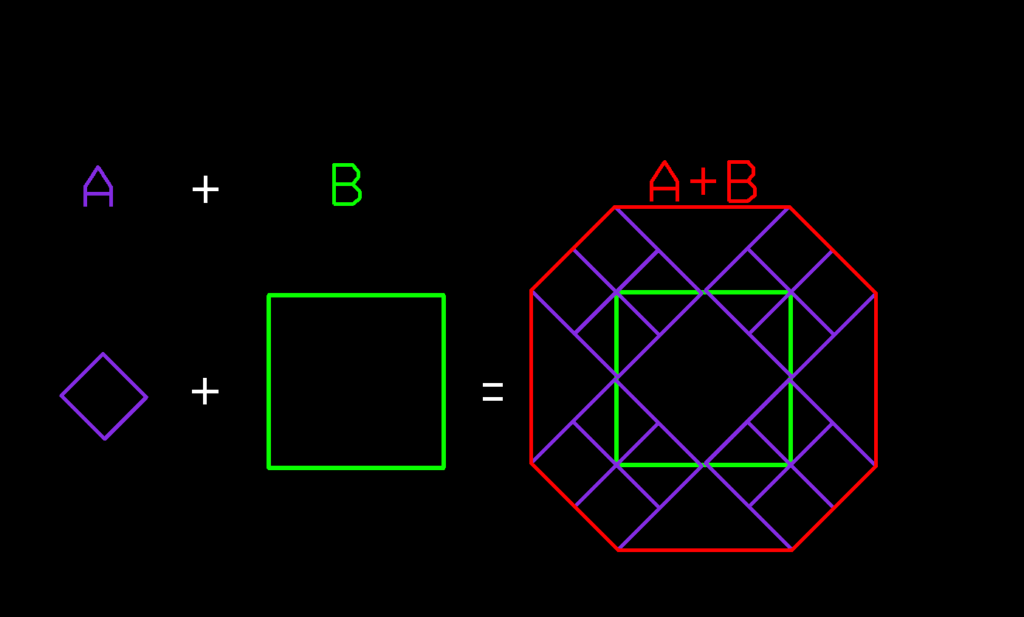
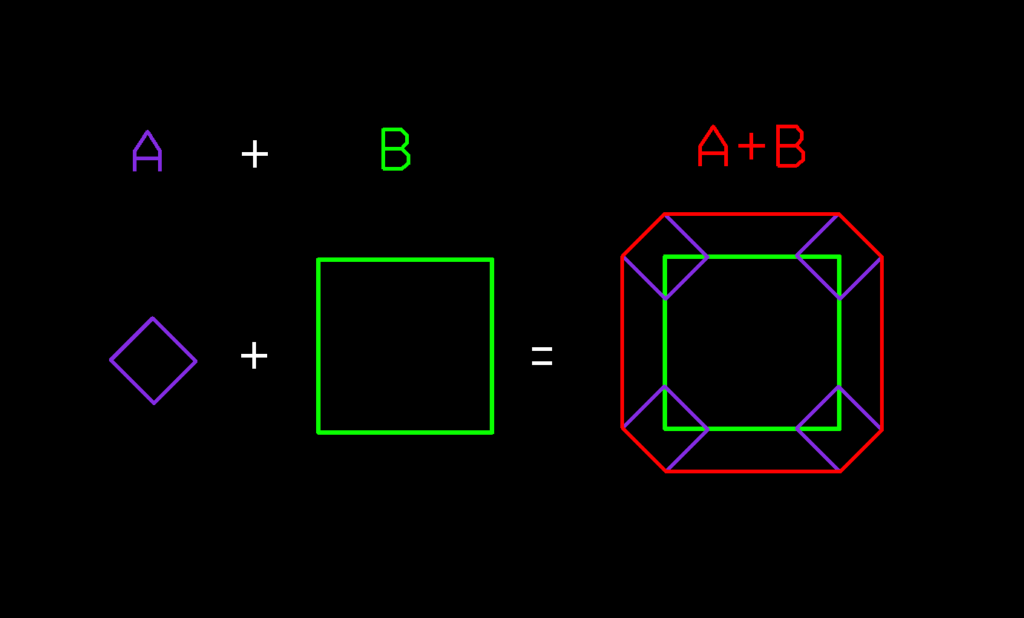
1- Minkowski Sums of two polygons is defined as a set of points computed by summing all pairs of points from the 2 polygons.

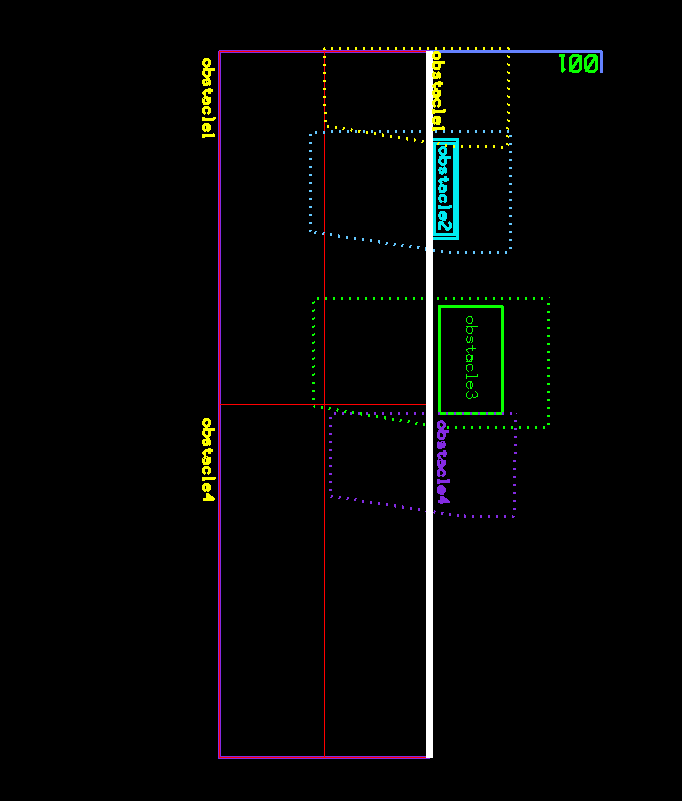
2- A convex polygon is any shape that has all interior angles that measure less than 180 degrees. A Convex Hull is the smallest convex set that contains a given shape or set of points. Boost Geometry Library implements a straightforward method to compute a Convex Hull for a set of supported geometries. Following are the Convex Hulls for our label and obstacles:

Computing the collision-free space for the new label

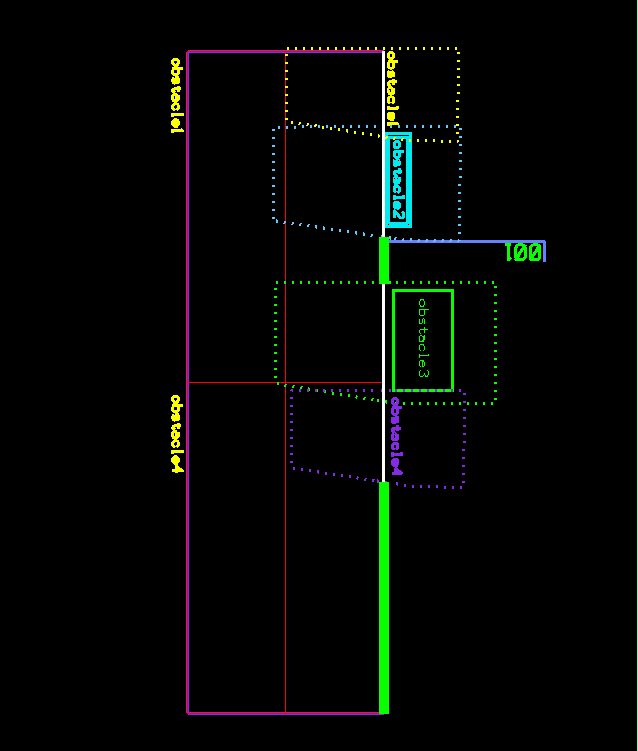
We’re using the following steps to compute the collision-free space for the “001” in the example above:

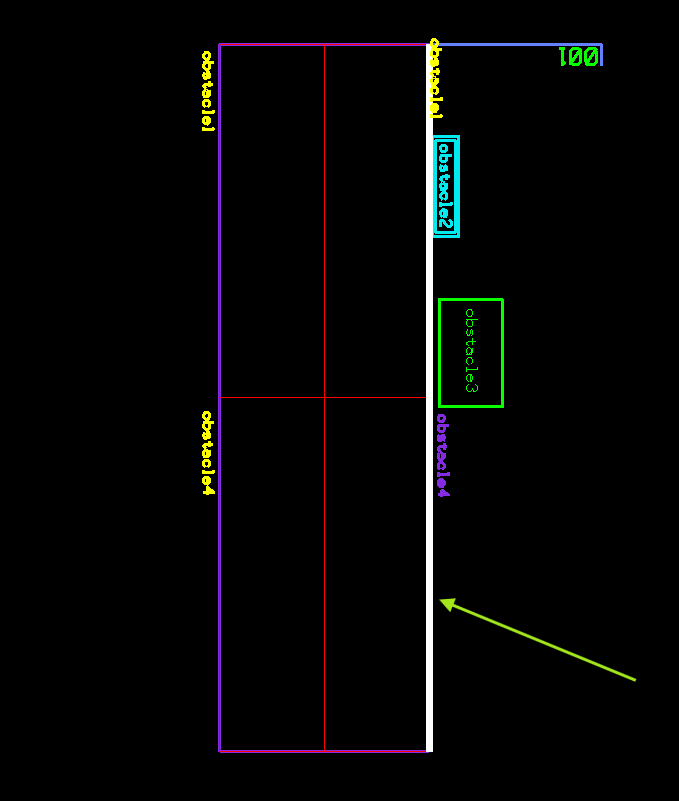
1- Translate our items to the (0,0) origin and rotate them by 180°.

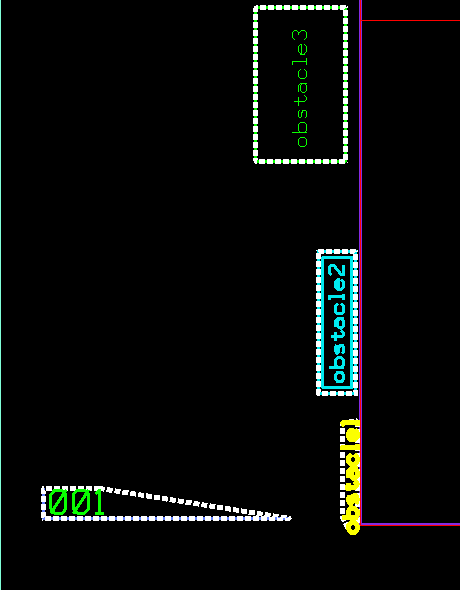
2- Extract the main placement line (shown in white below) that represents all possible placement points, with or without collision with any existing objects.

3- Compute the Minkowski Sums of the Convex hull of the “001” label with each obstacle. Results are shown in dashed polygons in the image below.

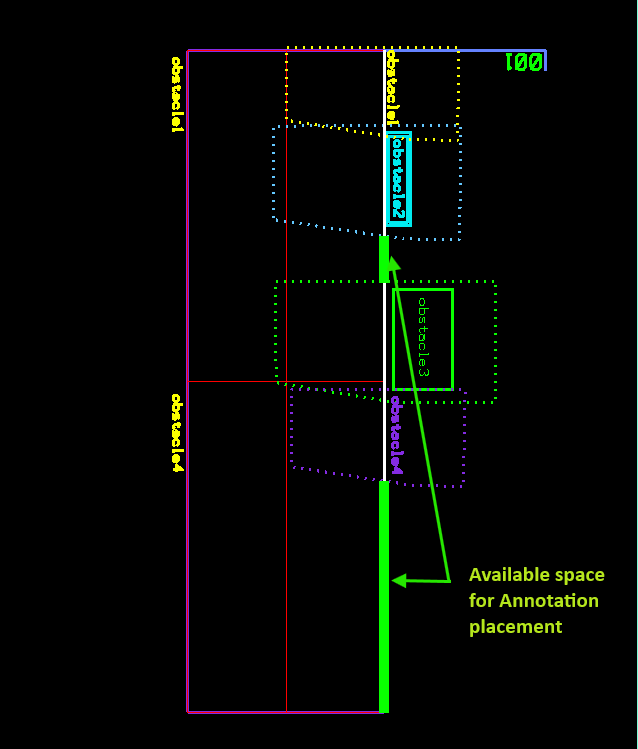
4- Clip the Minkowski Sums out of the main placement line as the resulting shapes represent the collision space.

5- Place label on any point on the segments resulting from clipping the collision space from the main placement line (shown in green below). For simplicity, we will pick the point closest to beginning of the side line.

Sample code

Here’s sample code from Boost Geometry Library website to compute the convex hull of a polygon:

#include <iostream>

#include <boost/geometry.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/adapted/boost_tuple.hpp>

BOOST_GEOMETRY_REGISTER_BOOST_TUPLE_CS(cs::cartesian)


int main()
{
    typedef boost::tuple<double, double> point;
    typedef boost::geometry::model::polygon<point> polygon;

    polygon poly;
    boost::geometry::read_wkt("polygon((2.0 1.3, 2.4 1.7, 2.8 1.8, 3.4 1.2, 3.7 1.6,3.4 2.0, 4.1 3.0"
        ", 5.3 2.6, 5.4 1.2, 4.9 0.8, 2.9 0.7,2.0 1.3))", poly);

    polygon hull;
    boost::geometry::convex_hull(poly, hull);

    using boost::geometry::dsv;
    std::cout
        << "polygon: " << dsv(poly) << std::endl
        << "hull: " << dsv(hull) << std::endl
        ;


    return 0;
}

The following code computes the Minkowski Sums of a set of obstacle polygons using the Boost Geometry Library convolve_two_polygon_sets().

/***************************************
  Descr: Returns the Minkowski Sums between a robot and and set of obstacles
****************************************/
int mcs_minkowskiSums 
(
 std::vector<point> pts_robot,		//  => flag hull pts [MU]
 vector<VecMsPoints>	vvObstaclePts,  //  => obstacle pts [MU]
 vector<VecMsPoints>&	rvvMinSums		// <= 
)
{
	polygon_set a, b, c;
	polygon poly;
	
	removeObstacleIntersections(vvObstaclePts);

  // build polygon_set a that contains robots
	boost::polygon::set_points(poly, pts_robot.begin(), pts_robot.end());
	poly.size();
	a += poly;

   // build polygon_set b that contains obstacles
	for each (std::vector<point> pts in vvObstaclePts)
	{
		boost::polygon::set_points(poly1, pts.begin(), pts.end());
		poly1.size();
		b += poly1;
	}
 
  // Compute Minkowski Sums of the polygon sets a,b using Boost method 'convolve_two_polygon_sets'
	convolve_two_polygon_sets(c, a, b); // 

	using namespace boost::polygon;
	vector<polygon> resultPolygons;
	c.get(resultPolygons);
	
	return TRUE;
}

Conclusion

We have shown how to automatically add a new label to a CAD file without collision with existing items using Minkowski Sums and Convex hulls to find the collision space between the label and the obstacles. The application of this concept can extend beyond CAD/Collision Detection and can be used in numerous other fields such as robot motion, 3D modeling, and numerical control machining.

Mill Creek Systems, Inc provides software development services in this area. If you have any software needs, please reach out to us by clicking on the “Contact us” button below.

Helpful links:

Minkowski Sums Definition: https://cp-algorithms.com/geometry/minkowski.html

Introduction to Computational Geometry: https://www.geeksforgeeks.org/what-is-computational-geometry-and-how-is-it-applied-in-solving-geometric-problems

Minkowski Sums Tutorial in Boost Library https://www.boost.org/doc/libs/develop/libs/polygon/doc/gtl_minkowski_tutorial.htm

Convex Hulls https://en.wikipedia.org/wiki/Convex_polygon