October 2024 - Custom Software Development

Using Voronoi Diagrams to Equally Divide/Allocate Space Between Polygons

Problem description

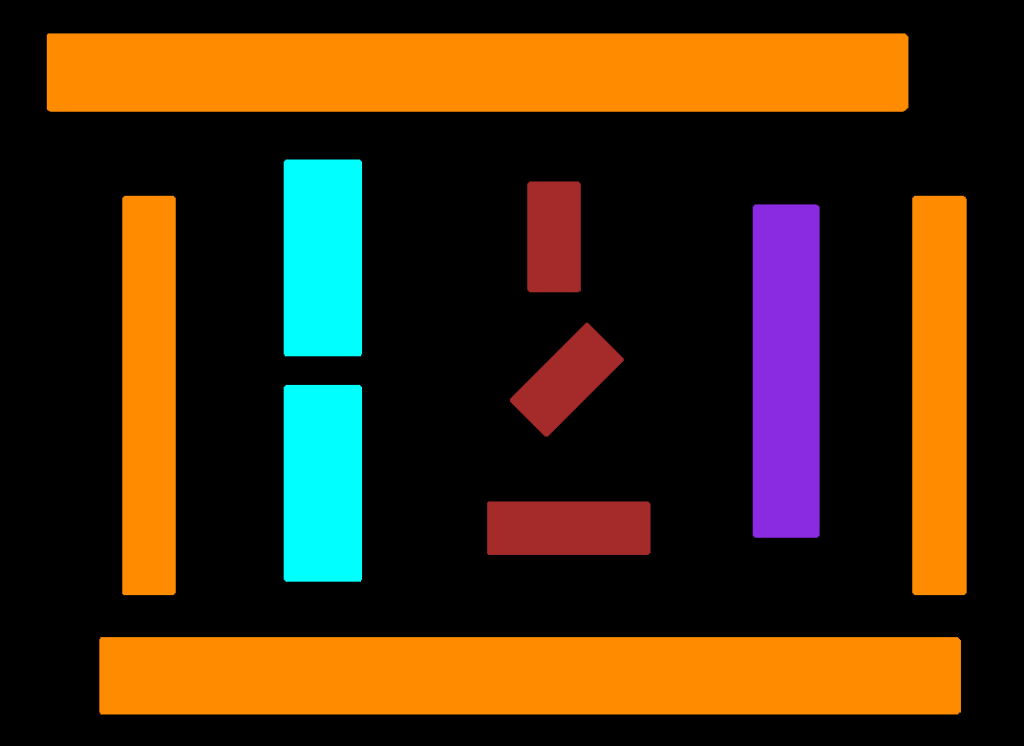
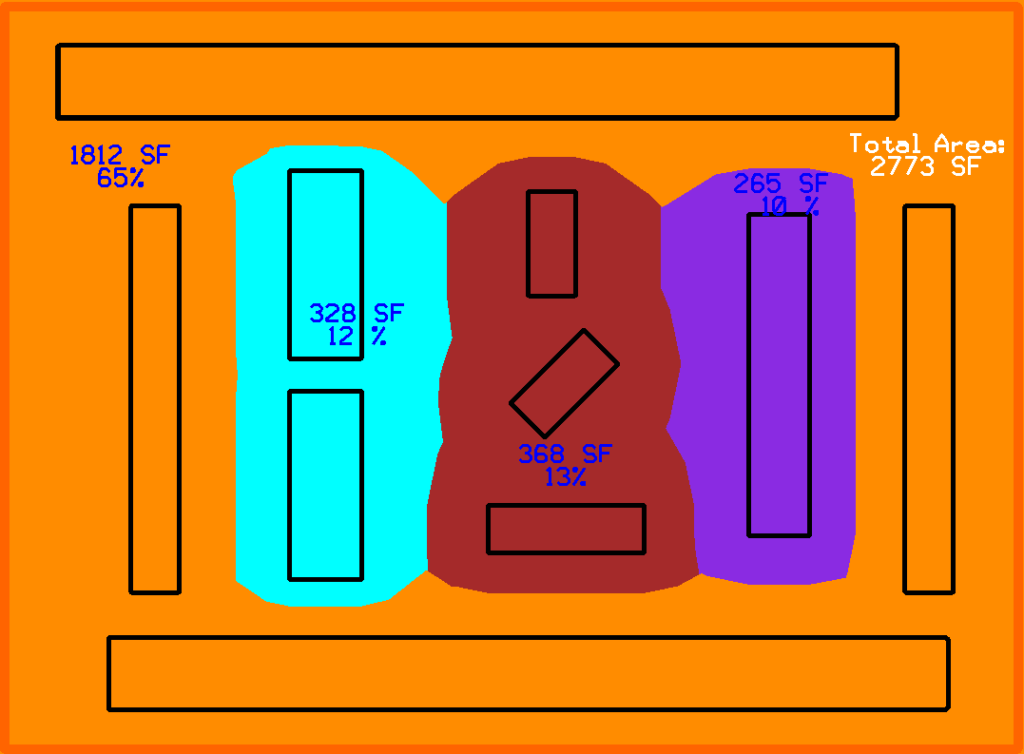
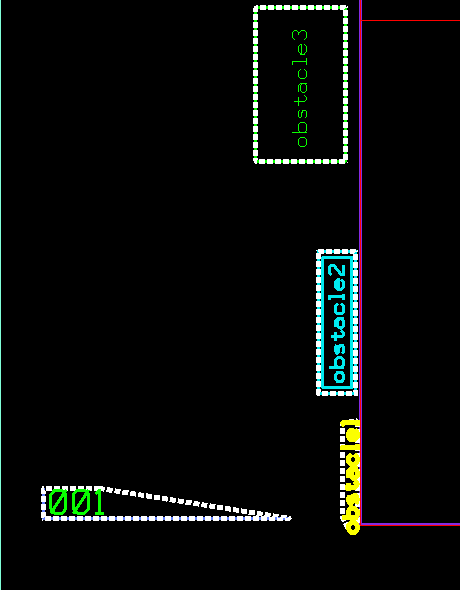
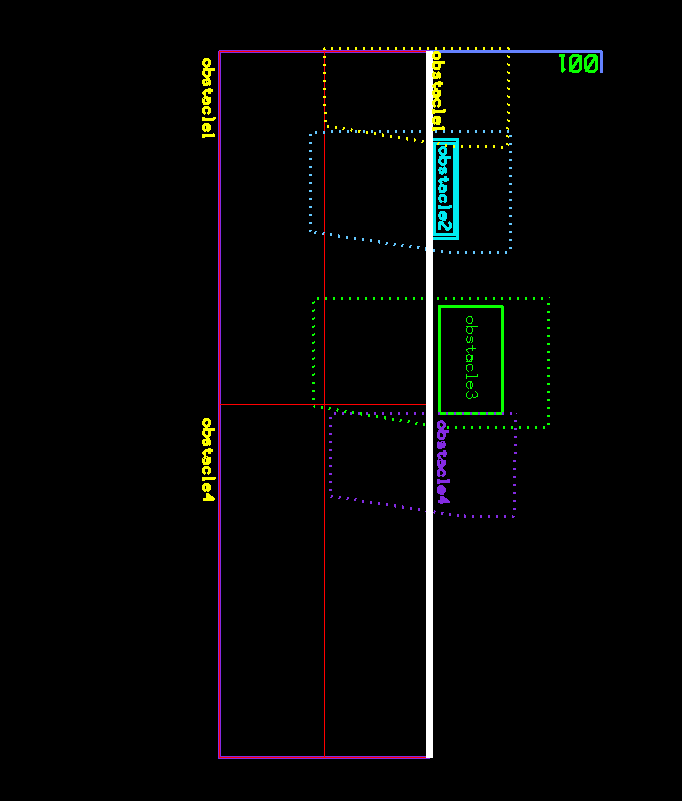
Given a set of arbitrary polygons belonging to different categories, we want to equally divide the space between the polygons and compute the square footage of each category. For example, given different categories of machines on a factory floor; for each category, we need to sum up the area of each machine polygon and its buffer zone and determine its percent in relation to the total factory floor area.

The following images show a set of polygons in different color-coded categories.

Arbitrary polygons with different color-coded categories.

Desired buffer polygons for each category.

Square footage of each category by percent of total area.

Introduction

We tried several approaches to compute the square footage including expanding the polygons until they intersect with each other and sending rays outward from each polygon to find midpoints with direct neighbors. Neither of the two approaches was successful. We needed an algorithm to find the buffer zone for each polygon in such a way that it divides the space equally between all adjacent polygons.

How to divide space between a set of polygons

We found a concept in computational geometry called Voronoi Diagrams. This allowed us to generate a set of midpoints between each polygon and all of its neighboring polygons. By creating a shape from the set of midpoints, we would find the center lines for each polygon as shown in the image below:

Voronoi Diagrams

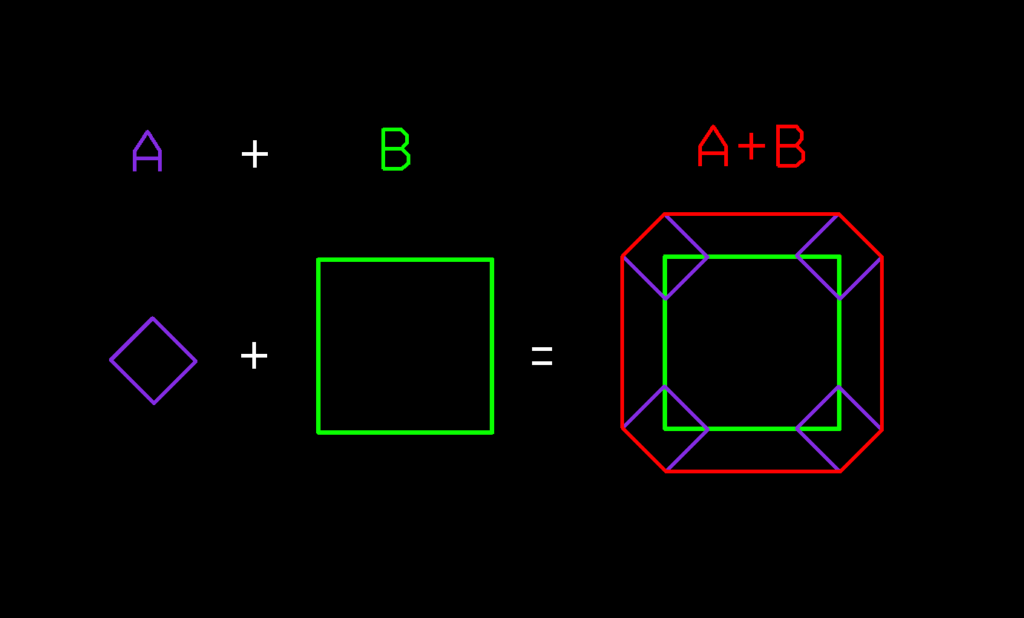
The simplest definition of Voronoi Diagrams is it being the partition of a plane into a set of regions close to each of a set of objects (seeds). In other words, given a set of seeds in a plane, a Voronoi region/cell of a seed is an area encompassing points closer to that seed than any other.

To use Voronoi Diagrams with a set of polygons, we need to compute a cell for each segment of a given polygon. By performing a union on the resulting Voronoi cells for each polygon, we find the center lines between the polygon and its direct neighbors (See examples below).

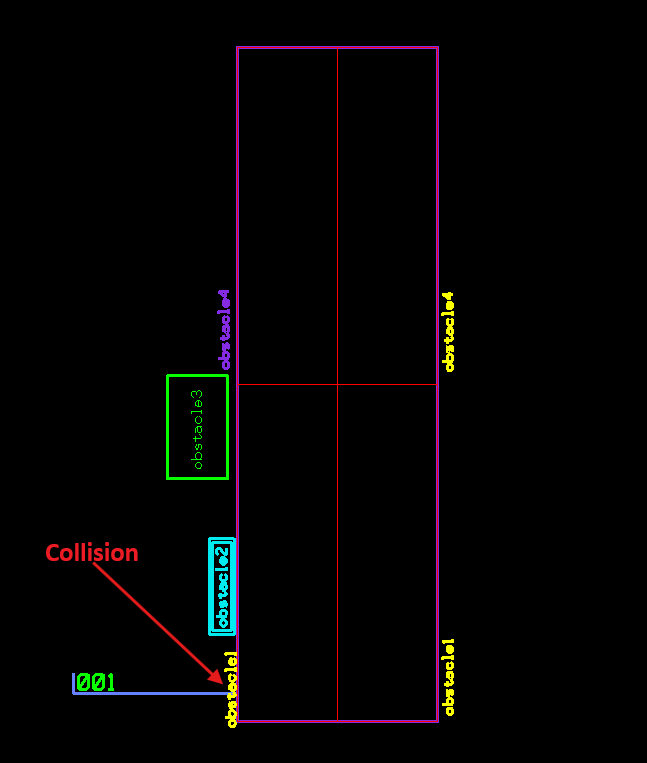
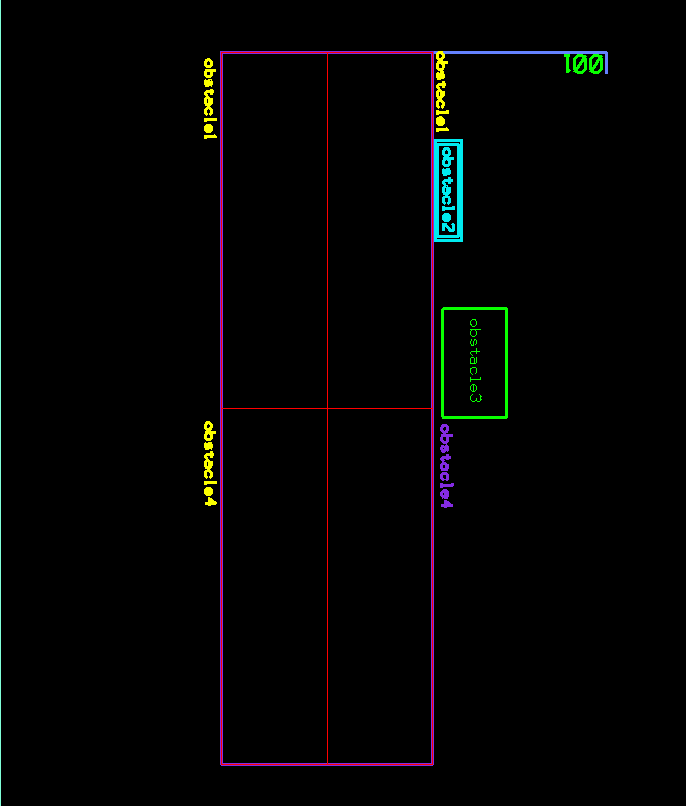
Following image shows a Voronoi cell for each segment with matching colors:

Voronoi Cells/Segments with matching colors

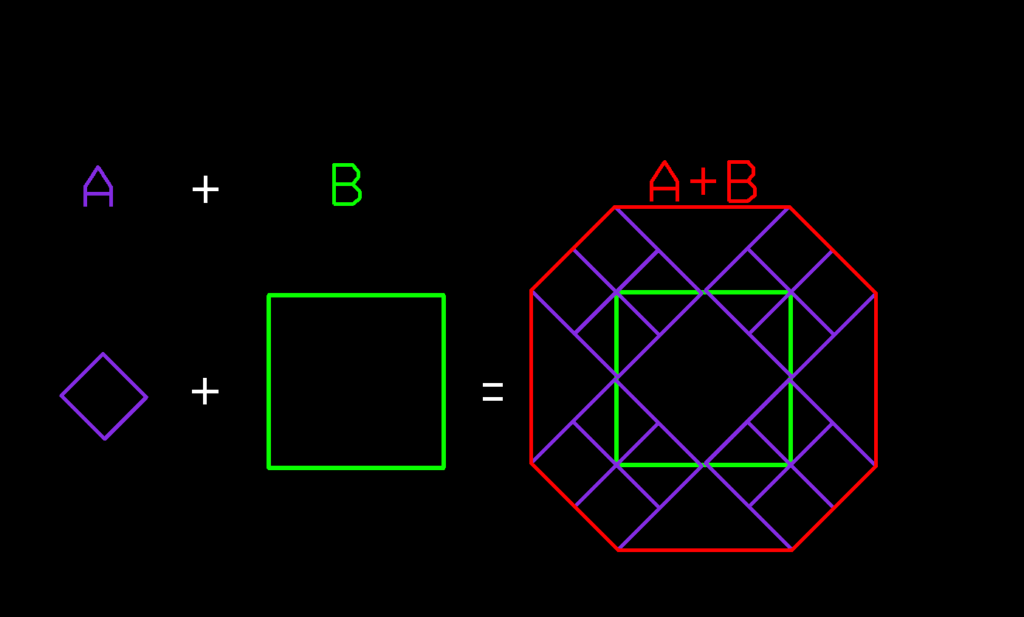
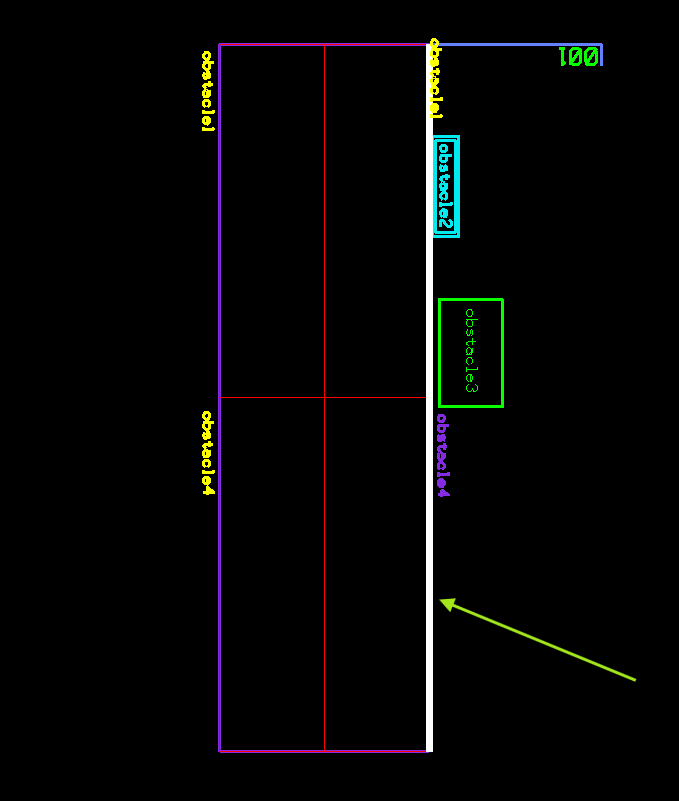
Following images show the Voronoi cells (in red) for each segment of two adjacent polygons and the final center lines in purple after performing the union of the Voronoi cells for each polygon:

All Voronoi cells (in red) for each
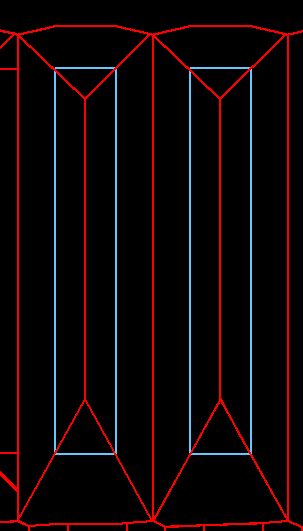
polygon

Voronoi cells combined with geometric
union to form center lines (in purple)

While performing a geometric union of the output Voronoi cells that resulted in center lines, we determined these center lines could be useful for other purposes such as navigation, routing, etc.

Step-by-step process of finding the center lines

Extract endpoints of all polygon segments
Assign segments a unique id to associate them with their original polygon
Use Boost Geometry Library to compute Voronoi cells for each segment
Identify all segments of the same polygon and perform a boolean union of the cells associated with them

The Boost Library provides a very efficient and easy-to-use function to compute the Voronoi Diagrams of any set of non-intersecting segments. By passing the segments of each polygon to the Boost Library, we’re computing the Voronoi cell for each segment. We’re then performing a boolean union of all resulting Voronoi cells for each polygon. As mentioned before, the union will be a shape representing the center lines between the polygon and its direct neighbors.

In the following C++ example, our polygons are stored in a collection called vPolygons. Also, segments are instances of the Segment_vd class which takes the coordinates of the segment endpoints and the index of the containing polygon as inputs to the constructor.

 // building a collection of segments from each polygon 
 // for each polygon
	for (unsigned index_polygon=0; index_polygon<vPolygons.size(); index_polygon++)
	{
		Polygon poly = vPolygons[index_polygon];

   // for each segment in current polygon
		for (int i=0; i< poly.numPnts; i++)
		{
			int curr = i, next = i==poly.numPnts-1?0:i+1;
			DPoint3d currP=poly.shapePnts[curr];
			DPoint3d nextP=poly.shapePnts[next];
    
      // add segment to collection with id = index_polygon
			segments.push_back(Segment_vd(currP.x, currP.y, nextP.x, nextP.y, index_polygon));	
		}
	}

	// Construction of the Voronoi Diagram.
	voronoi_diagram<double> vd;
	construct_voronoi(points.begin(), points.end(), segments.begin(), segments.end(),	&vd);

Conclusion

Voronoi Diagrams provide a straightforward method to computationally divide/allocate space between an arbitrary set of polygons.

Mill Creek Systems, Inc provides software development services in this area. If you have any software needs, please reach out to us by clicking on the “Contact us” button below.

Helpful links on Voronoi Diagrams:

Voronoi Diagrams Tutorial from Boost Geometry Library: https://www.boost.org/doc/libs/1_80_0/libs/polygon/doc/voronoi_diagram.htm

Interactive Voronoi Diagram Generator: https://alexbeutel.com/webgl/voronoi.html

Wolfram Definition of Voronoi Diagrams: https://mathworld.wolfram.com/VoronoiDiagram.html

Automating Label Placement in CAD Drawings Using Minkowski Sums and Convex Hulls for Obstacle Detection

Problem Description

Placing labels and annotations in CAD drawings is typically a very tedious/manual and error prone process. Automating the placement of the label itself is relatively straightforward, but determining where to place it without interfering with existing graphical entities is an entirely new problem to solve.

*“001”* label doesn’t intersect any existing items

Overview

To compute the collision-free placement of the new label for the example above we have developed a five step process outlined below using the Minkowski Sums and Convex Hulls algorithms from the Boost Geometry Library.

Quick definitions

1- Minkowski Sums of two polygons is defined as a set of points computed by summing all pairs of points from the 2 polygons.

Minkowski Sums of *A, B* with center of A as reference point

2- A convex polygon is any shape that has all interior angles that measure less than 180 degrees. A Convex Hull is the smallest convex set that contains a given shape or set of points. Boost Geometry Library implements a straightforward method to compute a Convex Hull for a set of supported geometries. Following are the Convex Hulls for our label and obstacles:

Convex Hulls of the new label and obstacles

Computing the collision-free space for the new label

We’re using the following steps to compute the collision-free space for the “001” in the example above:

1- Translate our items to the (0,0) origin and rotate them by 180°.

Items translated to (0,0) origin and rotated by 180°

2- Extract the main placement line (shown in white below) that represents all possible placement points, with or without collision with any existing objects.

Main placement line shown in white. This represents all placement points with or without collision

3- Compute the Minkowski Sums of the Convex hull of the “001” label with each obstacle. Results are shown in dashed polygons in the image below.

Dashed polygons being the Minkowski Sums of label and each obstacle

4- Clip the Minkowski Sums out of the main placement line as the resulting shapes represent the collision space.

All collision-free placement points on the 2 green segments

5- Place label on any point on the segments resulting from clipping the collision space from the main placement line (shown in green below). For simplicity, we will pick the point closest to beginning of the side line.

*“001”* label placed on first valid collision-free point

Sample code

Here’s sample code from Boost Geometry Library website to compute the convex hull of a polygon:

#include <iostream>

#include <boost/geometry.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/adapted/boost_tuple.hpp>

BOOST_GEOMETRY_REGISTER_BOOST_TUPLE_CS(cs::cartesian)


int main()
{
    typedef boost::tuple<double, double> point;
    typedef boost::geometry::model::polygon<point> polygon;

    polygon poly;
    boost::geometry::read_wkt("polygon((2.0 1.3, 2.4 1.7, 2.8 1.8, 3.4 1.2, 3.7 1.6,3.4 2.0, 4.1 3.0"
        ", 5.3 2.6, 5.4 1.2, 4.9 0.8, 2.9 0.7,2.0 1.3))", poly);

    polygon hull;
    boost::geometry::convex_hull(poly, hull);

    using boost::geometry::dsv;
    std::cout
        << "polygon: " << dsv(poly) << std::endl
        << "hull: " << dsv(hull) << std::endl
        ;


    return 0;
}

The following code computes the Minkowski Sums of a set of obstacle polygons using the Boost Geometry Library convolve_two_polygon_sets().

/***************************************
  Descr: Returns the Minkowski Sums between a robot and and set of obstacles
****************************************/
int mcs_minkowskiSums 
(
 std::vector<point> pts_robot,		//  => flag hull pts [MU]
 vector<VecMsPoints>	vvObstaclePts,  //  => obstacle pts [MU]
 vector<VecMsPoints>&	rvvMinSums		// <= 
)
{
	polygon_set a, b, c;
	polygon poly;
	
	removeObstacleIntersections(vvObstaclePts);

  // build polygon_set a that contains robots
	boost::polygon::set_points(poly, pts_robot.begin(), pts_robot.end());
	poly.size();
	a += poly;

   // build polygon_set b that contains obstacles
	for each (std::vector<point> pts in vvObstaclePts)
	{
		boost::polygon::set_points(poly1, pts.begin(), pts.end());
		poly1.size();
		b += poly1;
	}
 
  // Compute Minkowski Sums of the polygon sets a,b using Boost method 'convolve_two_polygon_sets'
	convolve_two_polygon_sets(c, a, b); // 

	using namespace boost::polygon;
	vector<polygon> resultPolygons;
	c.get(resultPolygons);
	
	return TRUE;
}

Conclusion

We have shown how to automatically add a new label to a CAD file without collision with existing items using Minkowski Sums and Convex hulls to find the collision space between the label and the obstacles. The application of this concept can extend beyond CAD/Collision Detection and can be used in numerous other fields such as robot motion, 3D modeling, and numerical control machining.

Mill Creek Systems, Inc provides software development services in this area. If you have any software needs, please reach out to us by clicking on the “Contact us” button below.

Helpful links:

Minkowski Sums Definition: https://cp-algorithms.com/geometry/minkowski.html

Introduction to Computational Geometry: https://www.geeksforgeeks.org/what-is-computational-geometry-and-how-is-it-applied-in-solving-geometric-problems

Minkowski Sums Tutorial in Boost Library https://www.boost.org/doc/libs/develop/libs/polygon/doc/gtl_minkowski_tutorial.htm

Convex Hulls https://en.wikipedia.org/wiki/Convex_polygon

Monthly Archives October 2024

Recent Posts

Recent Comments

Archives

Categories

Meta

Using Voronoi Diagrams to Equally Divide/Allocate Space Between Polygons

Using Voronoi Diagrams to Equally Divide/Allocate Space Between Polygons

Problem description

Introduction

How to divide space between a set of polygons

Voronoi Diagrams

Step-by-step process of finding the center lines

Conclusion

Automating Label Placement in CAD Drawings Using Minkowski Sums and Convex Hulls for Obstacle Detection

Automating Label Placement in CAD Drawings Using Minkowski Sums and Convex Hulls for Obstacle Detection

Problem Description

Overview

Computing the collision-free space for the new label

Sample code

Conclusion