Using Voronoi Diagrams to Equally Divide/Allocate Space Between Polygons
Problem description
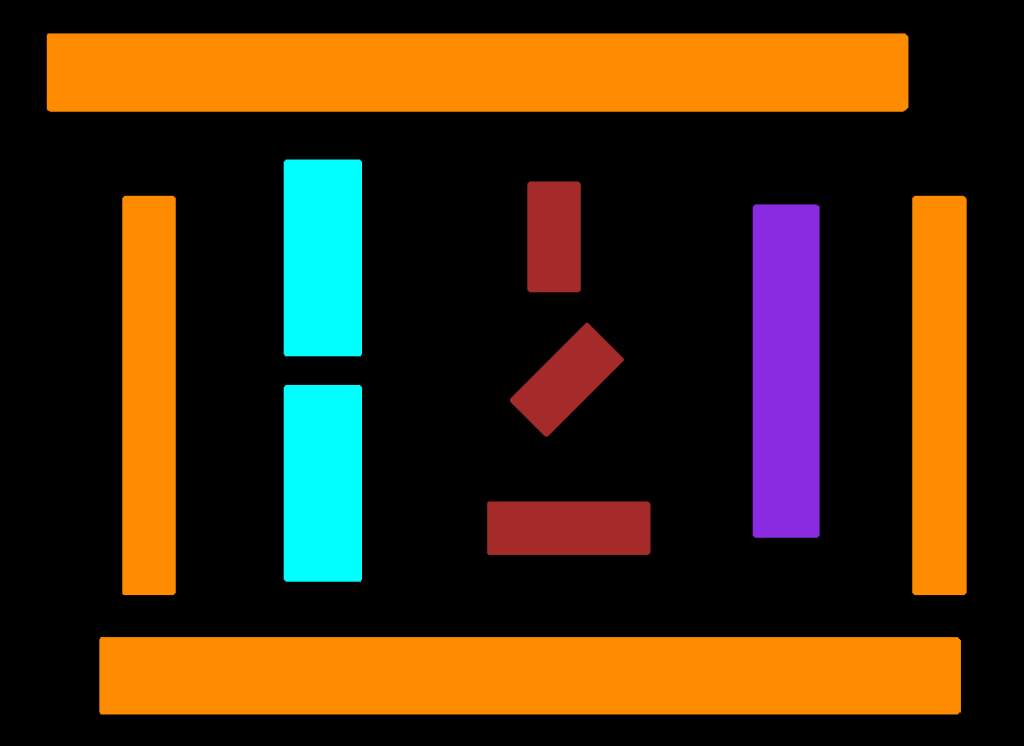
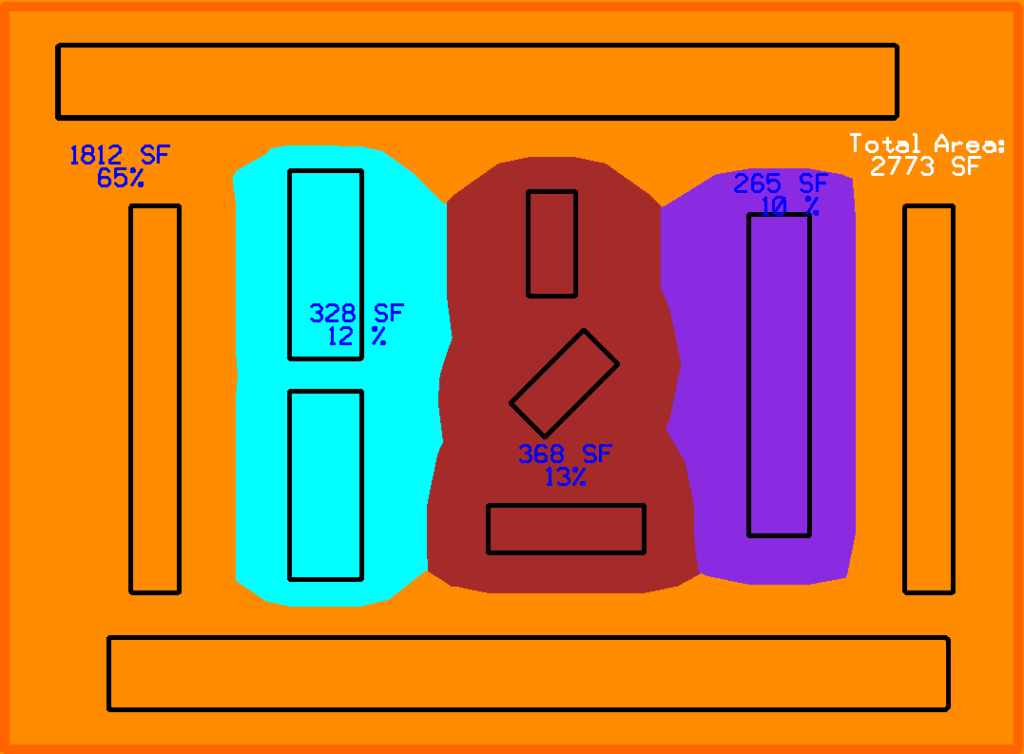
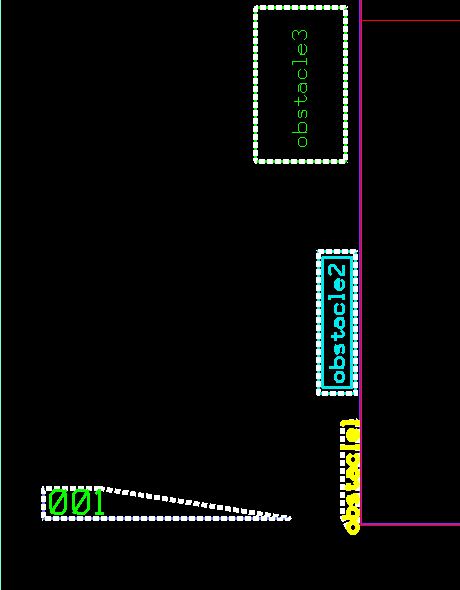
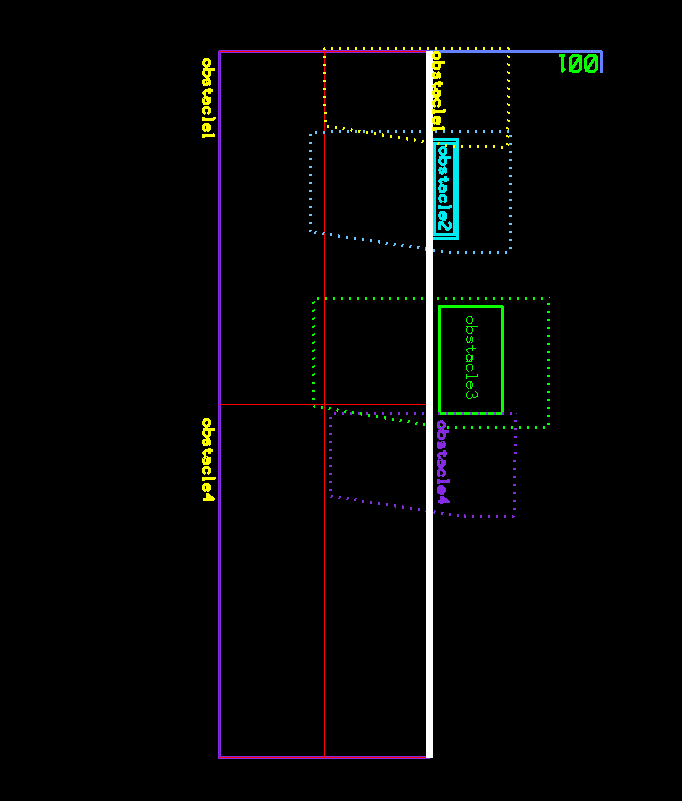
Given a set of arbitrary polygons belonging to different categories, we want to equally divide the space between the polygons and compute the square footage of each category. For example, given different categories of machines on a factory floor; for each category, we need to sum up the area of each machine polygon and its buffer zone and determine its percent in relation to the total factory floor area.
The following images show a set of polygons in different color-coded categories.
Introduction
We tried several approaches to compute the square footage including expanding the polygons until they intersect with each other and sending rays outward from each polygon to find midpoints with direct neighbors. Neither of the two approaches was successful. We needed an algorithm to find the buffer zone for each polygon in such a way that it divides the space equally between all adjacent polygons.
How to divide space between a set of polygons
We found a concept in computational geometry called Voronoi Diagrams. This allowed us to generate a set of midpoints between each polygon and all of its neighboring polygons. By creating a shape from the set of midpoints, we would find the center lines for each polygon as shown in the image below:
Voronoi Diagrams
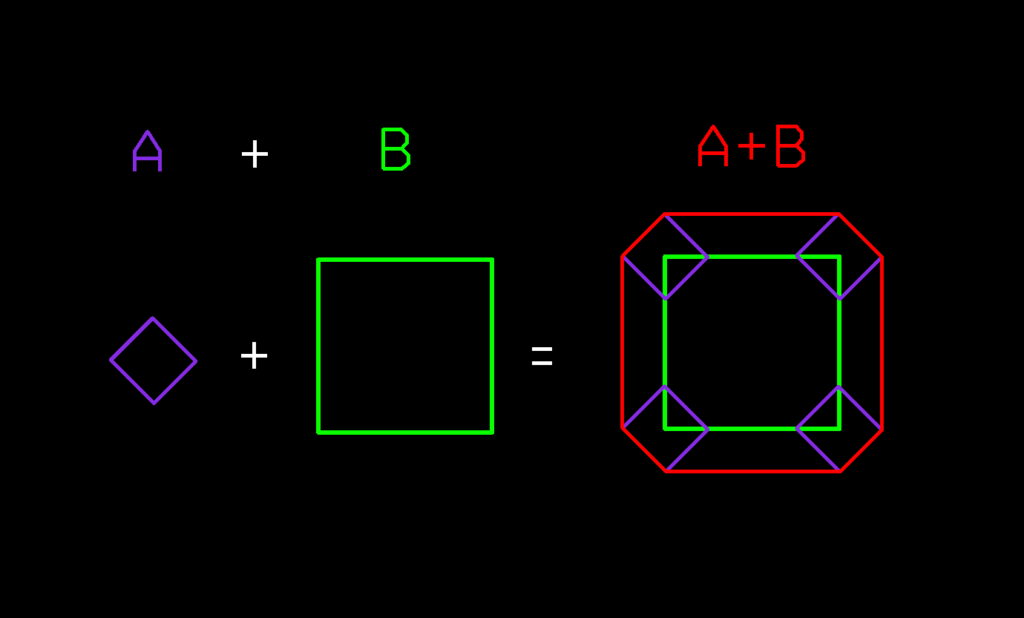
The simplest definition of Voronoi Diagrams is it being the partition of a plane into a set of regions close to each of a set of objects (seeds). In other words, given a set of seeds in a plane, a Voronoi region/cell of a seed is an area encompassing points closer to that seed than any other.
To use Voronoi Diagrams with a set of polygons, we need to compute a cell for each segment of a given polygon. By performing a union on the resulting Voronoi cells for each polygon, we find the center lines between the polygon and its direct neighbors (See examples below).
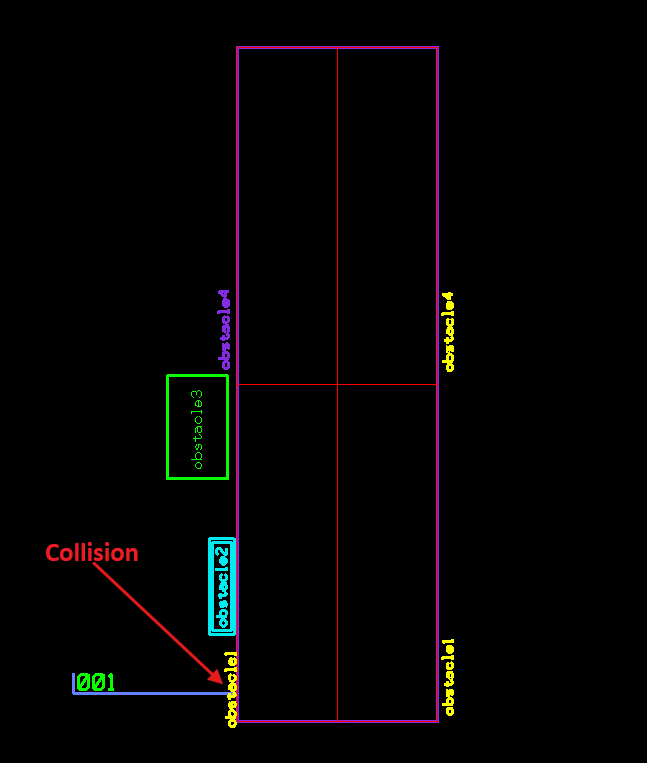
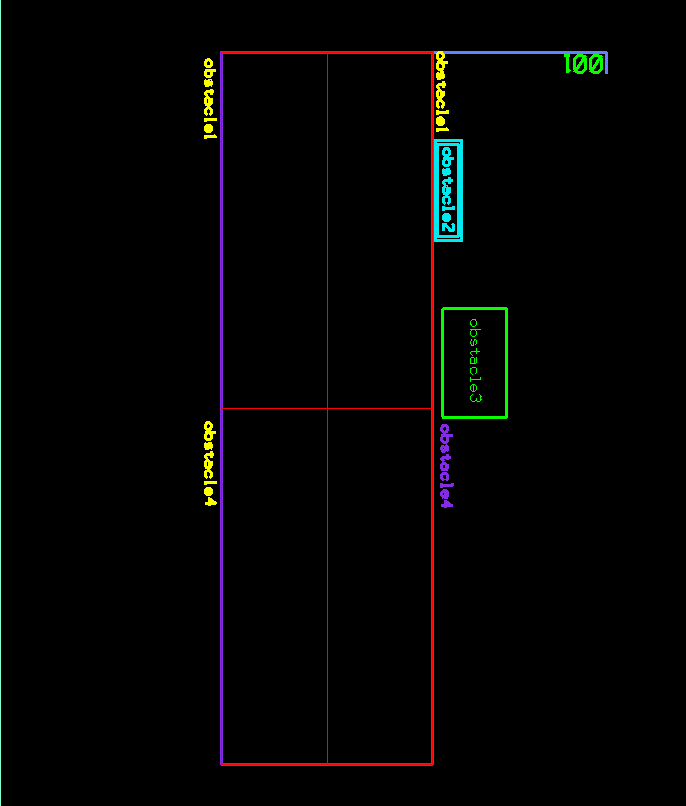
Following image shows a Voronoi cell for each segment with matching colors:
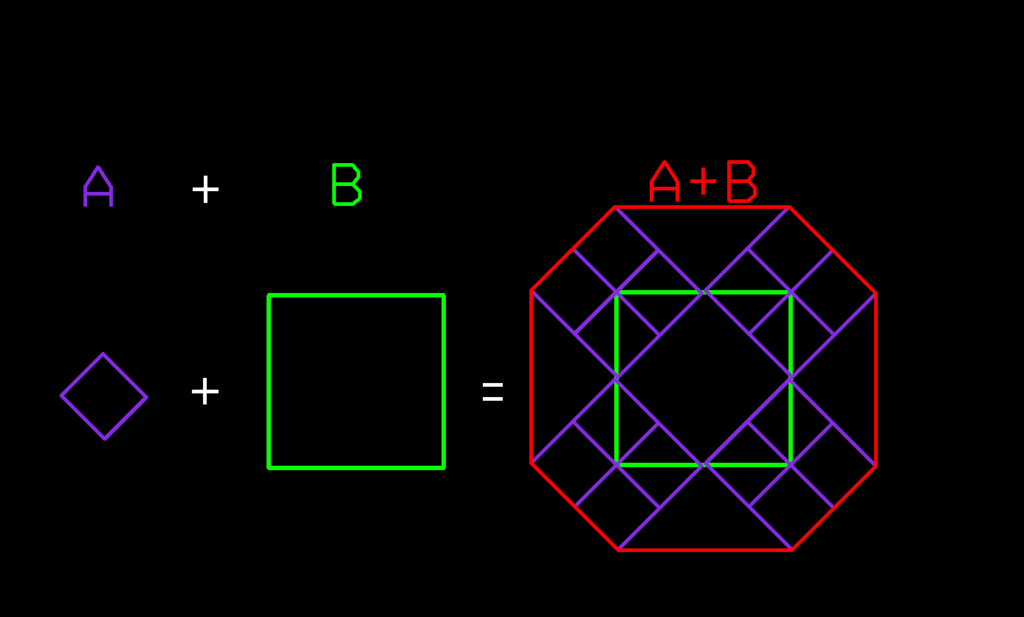
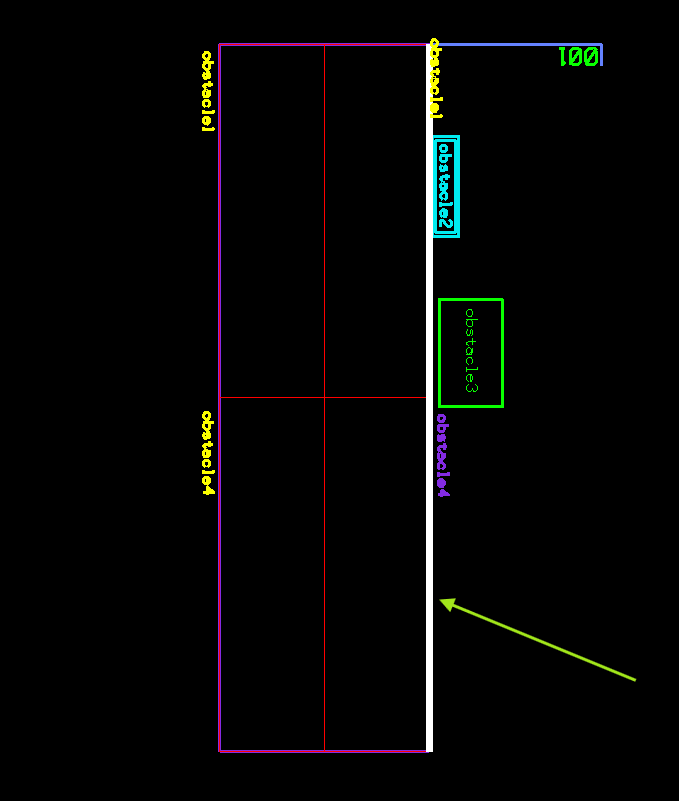
Following images show the Voronoi cells (in red) for each segment of two adjacent polygons and the final center lines in purple after performing the union of the Voronoi cells for each polygon:
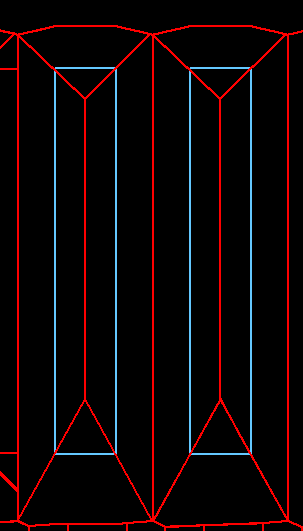
polygon

union to form center lines (in purple)
While performing a geometric union of the output Voronoi cells that resulted in center lines, we determined these center lines could be useful for other purposes such as navigation, routing, etc.
Step-by-step process of finding the center lines
- Extract endpoints of all polygon segments
- Assign segments a unique id to associate them with their original polygon
- Use Boost Geometry Library to compute Voronoi cells for each segment
- Identify all segments of the same polygon and perform a boolean union of the cells associated with them
The Boost Library provides a very efficient and easy-to-use function to compute the Voronoi Diagrams of any set of non-intersecting segments. By passing the segments of each polygon to the Boost Library, we’re computing the Voronoi cell for each segment. We’re then performing a boolean union of all resulting Voronoi cells for each polygon. As mentioned before, the union will be a shape representing the center lines between the polygon and its direct neighbors.
In the following C++ example, our polygons are stored in a collection called vPolygons. Also, segments are instances of the Segment_vd class which takes the coordinates of the segment endpoints and the index of the containing polygon as inputs to the constructor.
// building a collection of segments from each polygon
// for each polygon
for (unsigned index_polygon=0; index_polygon<vPolygons.size(); index_polygon++)
{
Polygon poly = vPolygons[index_polygon];
// for each segment in current polygon
for (int i=0; i< poly.numPnts; i++)
{
int curr = i, next = i==poly.numPnts-1?0:i+1;
DPoint3d currP=poly.shapePnts[curr];
DPoint3d nextP=poly.shapePnts[next];
// add segment to collection with id = index_polygon
segments.push_back(Segment_vd(currP.x, currP.y, nextP.x, nextP.y, index_polygon));
}
}
// Construction of the Voronoi Diagram.
voronoi_diagram<double> vd;
construct_voronoi(points.begin(), points.end(), segments.begin(), segments.end(), &vd);
Conclusion
Voronoi Diagrams provide a straightforward method to computationally divide/allocate space between an arbitrary set of polygons.
Mill Creek Systems, Inc provides software development services in this area. If you have any software needs, please reach out to us by clicking on the “Contact us” button below.
Helpful links on Voronoi Diagrams:
Voronoi Diagrams Tutorial from Boost Geometry Library: https://www.boost.org/doc/libs/1_80_0/libs/polygon/doc/voronoi_diagram.htm
Interactive Voronoi Diagram Generator: https://alexbeutel.com/webgl/voronoi.html
Wolfram Definition of Voronoi Diagrams: https://mathworld.wolfram.com/VoronoiDiagram.html
Continue Reading