Using Marshaling to Pass Data between
C# and Native Code (C/C++, Fortran)
Introduction
Does your C#/VB.NET managed code program need to call unmanaged (legacy) code routines in DLL‘s written in C/C++, Fortran, or Assembler ?
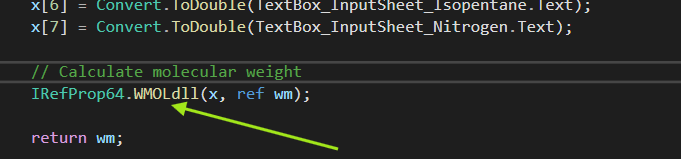
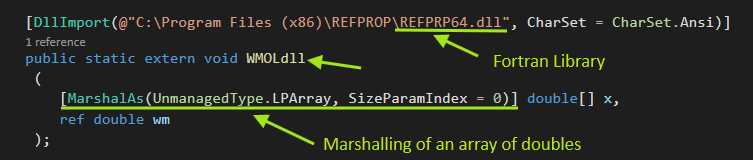
We found ourselves writing a C# program for a customer and needed to call analysis routines in a thermodynamics library called REFPROP which was written in Fortran and compiled with the C-Runtime library. The REFPROP routines expect character, integer, double arrays of data passed as both inputs and outputs. Types can be different (size, allocation, structure…etc) between managed and unmanaged code and hence the main need for marshaling as explained in this post. The following images show a Fortran method wrapped and invoked from within a C# program:
Overview
Marshaling in C# is the process of converting data between different languages and environments. One of its most important aspects is managing the data to be passed from unmanaged code to managed code and vice versa. Managed code is code that is handled by a runtime environment such as CLR (Common Language Runtime) whereas unmanaged code is code that is run directly on the hardware and outside any runtime environment. In C#, marshaling is often used to interact with native code, such as code written in C/C++ or Fortran. In this article, we will explain the basics of marshaling in C# and provide examples of how to make use of it.
Why is Marshaling needed ?
Marshaling is needed because the data types and memory are handled very differently between managed and unmanaged code. For example, a typical C-Runtime routine takes as both input/output a pointer to an array of characters, whereas C# provides a string class which does not give access to pointers. Thus, a mechanism is needed to pass data between managed and unmanaged environments. Types of parameters which do not require any conversion/marshaling, for instance int, double, byte, long, are called Blittable. Marshaling for Non-Blittable types in C# is achieved using the MarshalAs attribute. See example below:
Examples
To achieve marshaling in managed code (C#), we have to use the MarshalAsAttribute attribute. It can be applied to either fields of a class, parameters, or return values of a method:
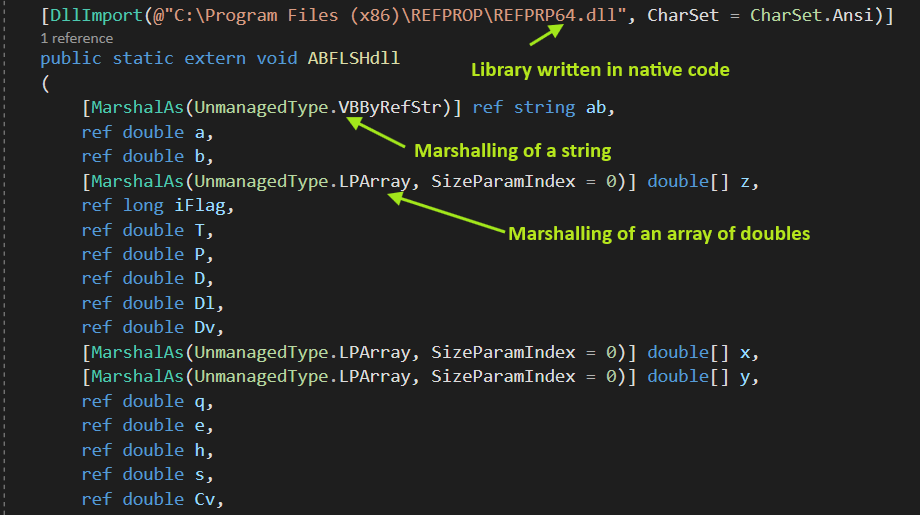
Marshaling of a parameter of a method:
[DllImport(@"C:\Program Files (x86)\REFPROP\REFPRP64.dll", CharSet = CharSet.Ansi)]
public static extern void ABFLSHdll
(
[MarshalAs(UnmanagedType.VBByRefStr)] ref string ab,
ref double a,
ref double b,
[MarshalAs(UnmanagedType.LPArray, SizeParamIndex = 0)] double[] z,
ref long iFlag,
ref double T,
ref double P,
ref double D,
ref double Dl,
ref double Dv,
[MarshalAs(UnmanagedType.LPArray, SizeParamIndex = 0)] double[] x,
[MarshalAs(UnmanagedType.LPArray, SizeParamIndex = 0)] double[] y,
ref double q,
ref double e,
ref double h,
ref double s,
ref double Cv,
ref double Cp,
ref double w,
ref long ierr,
[MarshalAs(UnmanagedType.VBByRefStr)] ref string herr,
ref long ab_length,
ref long herr_length
);
In the code above, the ABFLSHdll routine is being imported (first line) from a library (REFPRP64.dll) written in Fortran and takes strings and arrays among other types which don’t need to be marshaled in-between native and managed code namely: double, int, long parameters. The first parameter is a string and is being marshaled using [MarshalAs(UnmanagedType.VBByRefStr)]. The method also expects an array of doubles for the fourth parameter and is being marshaled using [MarshalAs(UnmanagedType.LPArray, SizeParamIndex = 0)].
Marshaling of a return value of a method:
[return: MarshalAs(UnmanagedType.LPWStr)]
public String SaySomething()
{
return "Hello World";
}
The return value of type String of the the function “SaySomething” above is marshaled using the keyword return: and the attribute MarshalAs(UnmanagedType.LPWStr).
Marshaling of a field of a class:
class MyClass {
[MarshalAs(UnmanagedType.LPWStr)]
public String msg = "Hello World";
}
The member field msg in the class above is marshaled using [MarshalAs(UnmanagedType.LPWStr)].
Conclusion
We’ve briefly explained Marshaling in this article and provided a few examples on how to do it in C#. As stated above, not all types need to be marshaled when importing unmanaged code. The MarshalAsAttribute is therefore optional as each data type has a default marshaling mechanism and the attribute is only necessary when a given type can be marshaled to multiple types within an environment.
Mill Creek Systems, Inc provides software development services in this area. If you have any software needs, please reach out to us by clicking on the “Contact us” button below.
Helpful links
Type marshaling in C#: https://learn.microsoft.com/en-us/dotnet/standard/native-interop/type-marshalling
Blittable and Non-Blittable types: https://learn.microsoft.com/en-us/dotnet/framework/interop/blittable-and-non-blittable-types
Common Language Runtime: https://learn.microsoft.com/en-us/dotnet/standard/clr?redirectedfrom=MSDN
Continue Reading