Using collision detection in a CAD Drawing to place non-intersecting elements.

Overview

The goal is to automate the placement of a label/cell in a CAD file without collision with preexisting items for legibility and presentation purposes. We will focus on CAD in this post and we’ll be using a light version of a concept in Computational Geometry called Minkowski Sums to detect obstacles. Please note that the application of this concept can extend beyond CAD and collision detection. It is also used in numerous other fields such as robot motion, 3D modeling, … etc

Illustrative Example

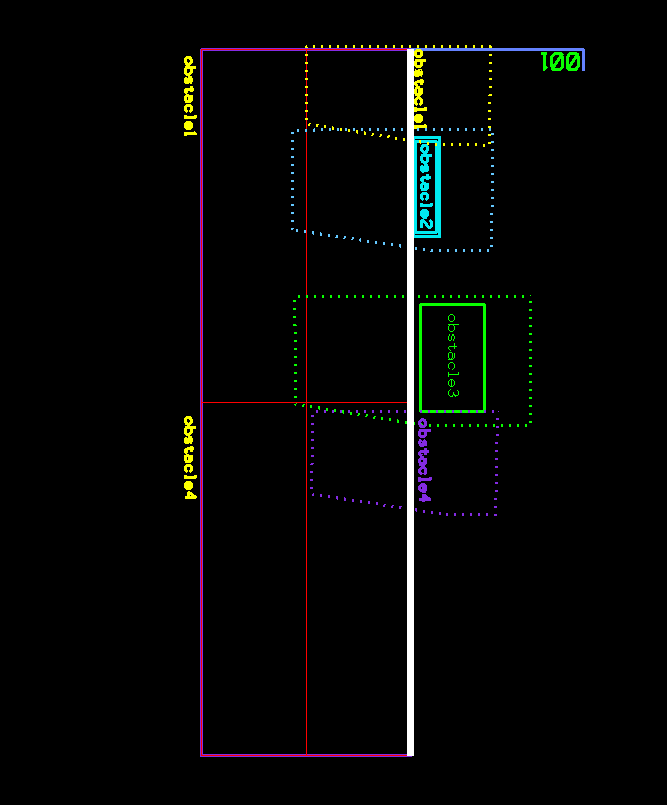
Given a CAD drawing of a cell with multiple labels placed on the side. Programmatically place a new label “001” without intersecting any preexisting labels/objects.

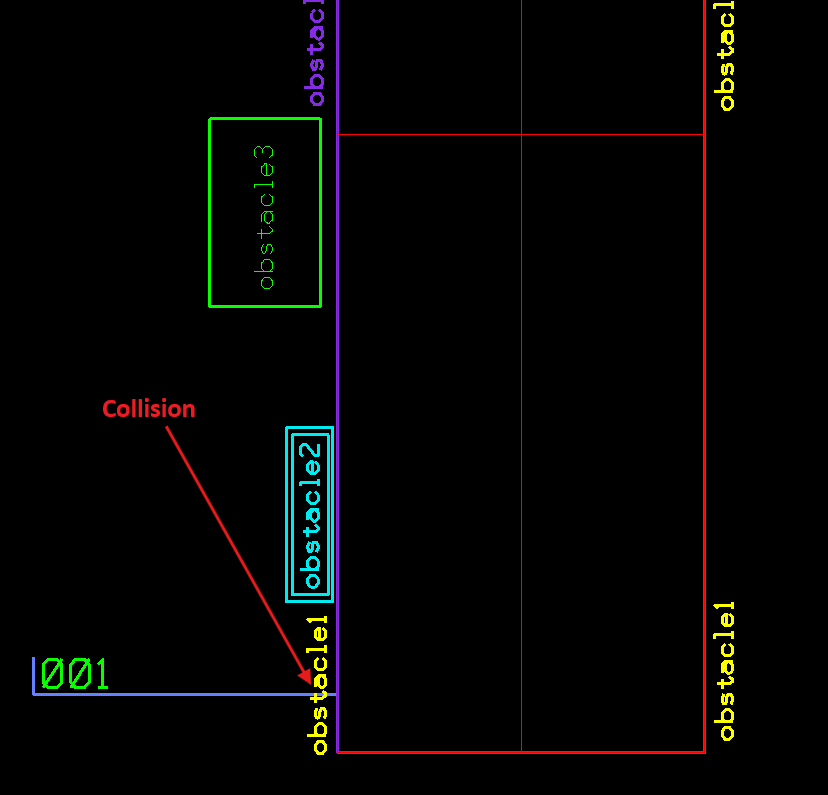
Collision between the “001” label and obstacle1

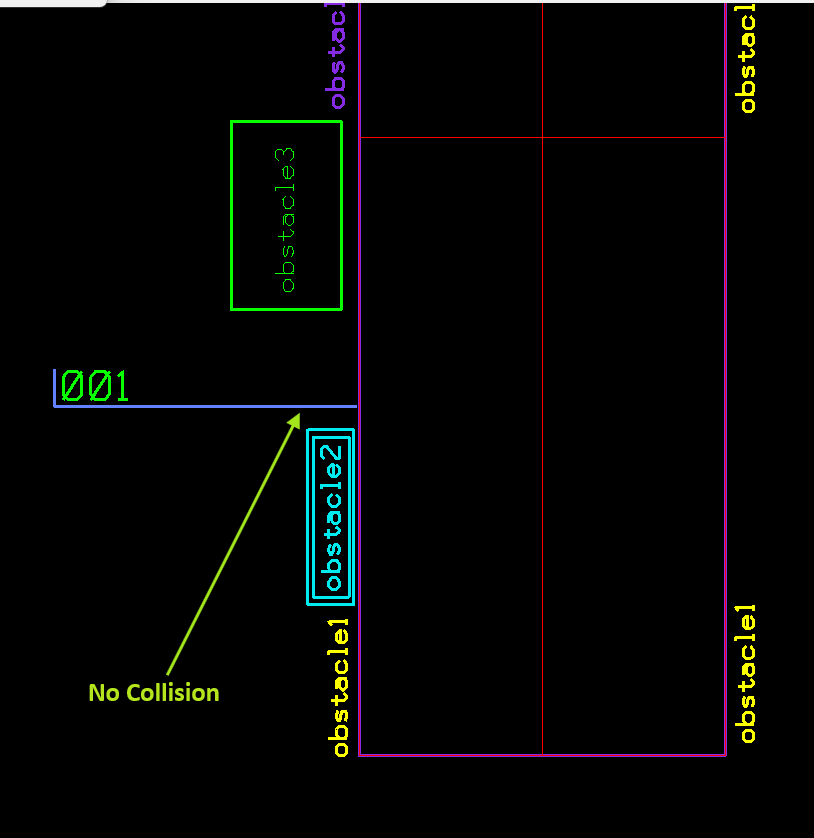
No collision between the “001” label and existing obstacles

Introduction

To achieve a collision-free placement of the new label for the example above, we’re using a concept in Computational Geometry called Minkowski Sums. Minkowski Sums of two polygons is defined as a set of points extracted by summing all pairs of points from the 2 polygons.

By creating a concave hull for each obstacle and the new label, we’re convolving the new label with each obstacle at 0,0 origin and 180°. The result of the convolution will represent the collision space for each obstacle and the new label can be placed anywhere outside of the collision space.

Quick Definitions

Please check out Boost library Minkowski Sums tutorial here

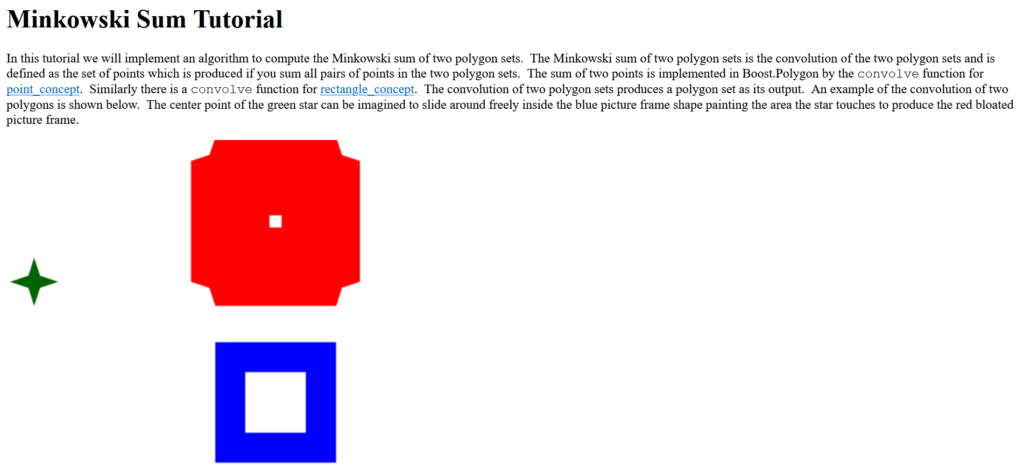
The center of the green shape (robot) in the illustration above has been overlapped with each vertex of the blue shape (obstacle). The resulting red shape is the space that the robot cannot cross to avoid colliding with the obstacle. The area outside of the red shape is the configuration space, the collision-free space where the robot can roam without colliding with the obstacles.

Computing the collision-free space for the “001” label in the example above

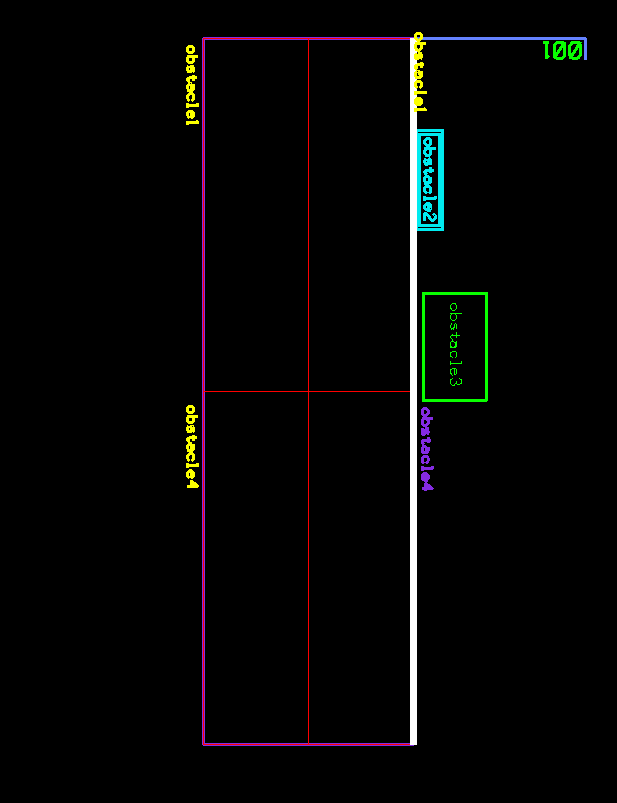
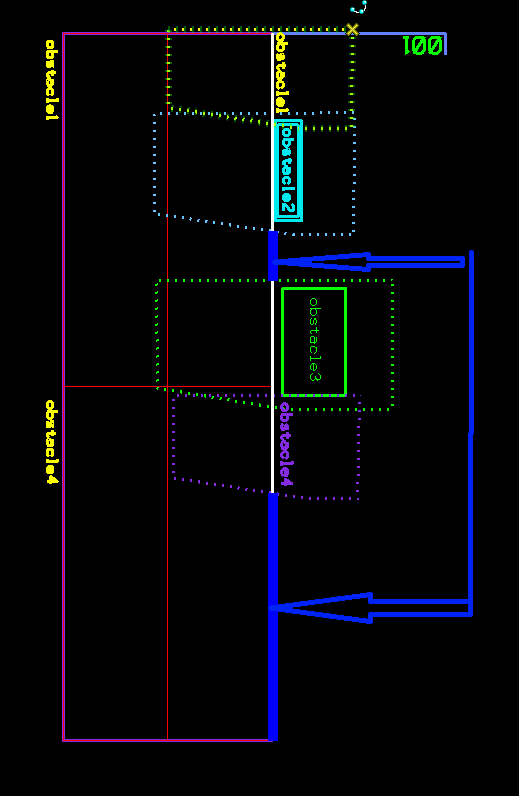
First step is to extract the main placement line (shown in white below) that represents all possible placement points, with or without collision with any existing objects. Then compute the Minkowski Sums of the “001” label with each obstacle at zero origin and at 180°. Results are shown in dashed polygons below. As explained before, the resulting shapes represent the collision space therefore they need to be clipped out of the white line. All the other points on the main placement line will be valid candidates for collision-free placement. For simplicity, we will pick the point closest to beginning of the side line.

Here’s a summary of the steps:

• Extract the main placement line
• Compute Minkowski Sums between label and obstacles at 0,0 org and at 180°
• Clip the resulting polygons from Minkowski Sums from the main placement line

Main placement line shown in White

Dashed polygons representing Minkowski Sums of label and each obstacle

Collision-free placement segments shown in blue

Sample code

/***************************************
  Descr: Returns the Minkowski Sums between a robot and and set of obstacles
****************************************/
int mcs_minkowskiSums 
(
 VecMsPoints			vRobotPts,		//  => flag hull pts [MU]
 vector<VecMsPoints>	vvObstaclePts,  //  => obstacle pts [MU]
 vector<VecMsPoints>&	rvvMinSums		// <= 
)
{
	polygon_set a, b, c;
	polygon poly;
	std::vector<point> pts_robot;

	removeObstacleIntersections(vvObstaclePts);

  // Convert robot points to UORs only necessary if you're using MDL (Bentley uStation)
	int index =0;
	for each (DPoint3d pt in vRobotPts) // convert to UORs
	{
		DPoint3d	dPt;
		Point3d		iPt;
		
		dPt.x = mdlCnv_masterUnitsToUors(pt.x);
		dPt.y = mdlCnv_masterUnitsToUors(pt.y);
		dPt.z = 0.0;

		mdlCnv_DPointToIPoint (&iPt, &dPt); 
		pts_robot.push_back(point(iPt.x,iPt.y));
	}

	boost::polygon::set_points(poly, pts_robot.begin(), pts_robot.end());
	//boost::geometry::correct(poly);
	poly.size();
	a += poly;

	for each (VecMsPoints vObstaclePts in vvObstaclePts)
	{
	  // Convert obtscale points to UORs. ** only necessary if you're using MDL (Bentley uStation)
		polygon poly1;
		std::vector<point> pts;
		for each (DPoint3d pt in vObstaclePts) // convert to UORs and * -1 for Mink Diff
		{
			DPoint3d	dPt;
			Point3d		iPt;
			
			dPt.x = mdlCnv_masterUnitsToUors(pt.x) * -1.0;
			dPt.y = mdlCnv_masterUnitsToUors(pt.y) * -1.0;
			dPt.z = 0.0;

			mdlCnv_DPointToIPoint (&iPt, &dPt); 
			
			pts.push_back(point(iPt.x,iPt.y));
		}

		boost::polygon::set_points(poly1, pts.begin(), pts.end());
		//boost::geometry::correct(poly1);
		poly1.size();
		b += poly1;
	}

	convolve_two_polygon_sets(c, a, b); // From Boost

	if (c.size() == 0)
		return FALSE;
	if (c.empty())
		return FALSE;

	//printf("\n BEFORE SIMPLE POLYGONS");
	//SimplePolygons simplePolygons;
	using namespace boost::polygon;
	vector<polygon> resultPolygons;
	c.get(resultPolygons);
	
	//for each(SimplePolygon poly in simplePolygons)
	for each(polygon poly in resultPolygons)
		rvvMinSums.push_back(mcs_get_points_poly(begin_points(poly), end_points(poly)));
	
	return TRUE;
}